Recall the Wien displacement law, which states that
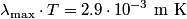 where 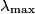 is the wavelength emitted by a blackbody at temperature is the wavelength emitted by a blackbody at temperature 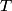 at which the intensity is a maximum. From this, we can easily find the temperature given the at which the intensity is a maximum. From this, we can easily find the temperature given the 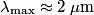 from the graph: from the graph: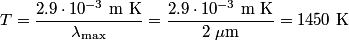 Therefore, answer (D) is correct. |